Metoda elementów skończonych
Kierunek:
Automatyka i Robotyka
Specjalność:
Modelowanie układów i procesów (AB3)
Rodzaj studiów i semestr: stacjonarne II st., sem. II
Punkty ECTS: 4
Prowadzący:
Prof. dr hab.
inż. Piotr Fedeliński
Opis przedmiotu
Metoda elementów skończonych (MES) jest powszechnie stosowaną metodą
komputerową analizy wytrzymałościowej układów odkształcalnych. Umożliwia
wyznaczenie przemieszczeń, odkształceń, naprężeń, reakcji podporowych i
innych wielkości w układach o złożonej geometrii i własnościach
materiałowych, obciążonych statycznie i dynamicznie. Rozwiązanie
numeryczne otrzymuje się w wyniku podziału obszaru ciała na elementy
skończone. W ramach przedmiotu będzie szczegółowo przedstawione
sformułowanie metody dla prętów i tarcz oraz zasady modelowania układów
elementami skończonymi. W ramach laboratorium studenci zapoznają się z
wykonywaniem obliczeń wytrzymałościowych za pomocą profesjonalnych
programów MES.
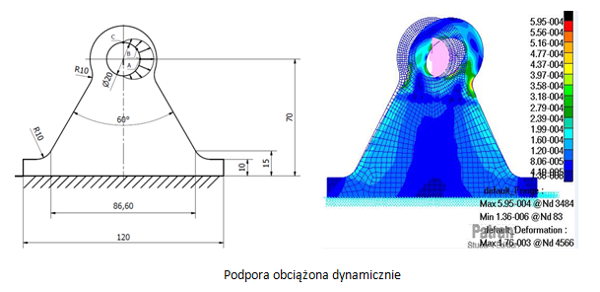
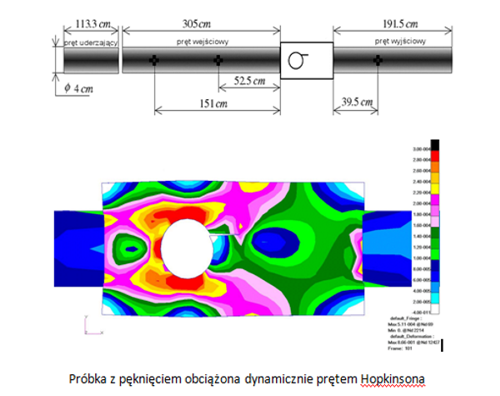
Program przedmiotu
- wykład: 30 godzin w semestrze
- laboratorium: 30 godzin w semestrze
Warunki zaliczenia
- Sprawozdania z
laboratorium.
- Sprawdziany
pisemne z wykładu i egzamin ustny
OCENA KOŃCOWA: O=0.7E+0.3C
E - ocena z wykładu L - ocena z laboratorium
Tematyka wykładów
-
Wprowadzenie: Oznaczenia i podstawowe
zależności. Energia potencjalna. Zasada
minimum energii potencjalnej. Metoda
Rayleigha-Ritza.
-
Zagadnienie jednowymiarowe: Podział na
elementy skończone. Funkcje kształtu.
Zależność między odkształceniami i
przemieszczeniami. Macierz sztywności
elementu. Siły objętościowe i
powierzchniowe. Tworzenie globalnej
macierzy sztywności i obciążenia.
Uwzględnienie warunków brzegowych.
-
Zagadnienie dwuwymiarowe: Element
trójkątny o stałym odkształceniu.
Funkcje kształtu. Reprezentacja
izoparametryczna. Zależność między
odkształceniami i przemieszczeniami.
Macierz sztywności elementu. Siły
objętościowe i powierzchniowe. Element
czworokątny czterowęzłowy. Całkowanie
numeryczne metodą Gaussa. Całkowanie
macierzy sztywności. Inne elementy
skończone.
-
Zagadnienie osiowo-symetryczne: Energia
potencjalna. Element trójkątny. Związki
między odkształceniami i
przemieszczeniami. Macierz sztywności
elementu. Siły objętościowe i
powierzchniowe.
-
Zasady
modelowania elementami skończonymi.
-
Metoda
elementów skończonych w analizie
dynamicznej: Rodzaje analizy
dynamicznej. Macierzowe równanie ruchu.
Sposoby tworzenia macierzy bezwładności.
Klasyfikacja metod całkowania
bezpośredniego. Metoda różnic
centralnych.
Tematyka laboratoriów
-
Przygotowanie danych do programów metody
elementów skończonych.
-
Analiza układów prętowych, tarcz i brył
metodą elementów skończonych.
-
Weryfikacja wyników obliczeń
numerycznych.
Literatura
- Rusiński E.,
Czmochowski J., Smolnicki T., Zaawansowana metoda
elementów skończonych w konstrukcjach nośnych, Oficyna
Wyd. Pol. Wroc., Wrocław, 2000.
- Kleiber M.,
Komputerowe metody mechaniki ciał stałych, Mechanika
techniczna, Tom XI, Wydawnictwo Naukowe PWN, Warszawa,
1995.
- Daćko M., Borkowski
W., Dobrociński S., Niezgoda T, Wieczorek M., Metoda
elementów skończonych w mechanice konstrukcji, Arkady,
Warszawa, 1994.
- Rakowski G., Kacprzyk
Z., Metoda elementów skończonych w mechanice
konstrukcji, Oficyna Wyd. Pol. Warszawskiej, Warszawa,
1993.
- Zienkiewicz O.C.,
Taylor R.L., The finite element method,
Butterworth-Heinemann, 2000.
- Chandrupatla T.R.,
Belegundu A.D., Introduction to finite element method in
engineering, Prentice-Hall International Editions, 1991.
- Cook R.D., Malkus
D.S., Plesha M.E., Concepts and applications of finite
element analysis, John Willey & Sons, New York, 1989.
- Weaver W., Johnston
P., Finite elements for structural analysis,
Prentice-Hall, Inc. Englewood Cliffs, New Jersey, 1984.
|