Modelowanie pól sprzężonych
Kierunek:
Mechanika i Budowa Maszyn
Specjalność:
Modelowanie i optymalizacja układów mechanicznych (MB4)
Rodzaj studiów i semestr: stacjonarne II st., sem. III
Punkty ECTS: 2
Prowadzący:
dr hab. inż. Adam Długosz
Opis przedmiotuW ramach
przedmiotu omawiane są wybrane zagadnienia sprzężone (ang. coupled
problems, multiphysics) wraz z omówieniem ich praktycznego
rozwiązania przy wykorzystaniu odpowiednich metod numerycznych.
Rozważane są głównie interakcje pomiędzy polami
mechanicznymi i niemechanicznymi. Omawiane problemy dotyczą zarówno
sprzężeń należących do klasy sprzężeń 'słabych' jak również i 'silnych'.
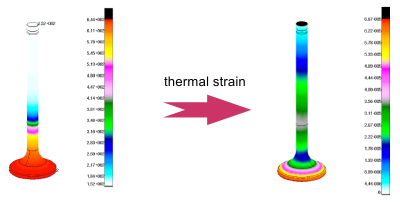
W ramach zajęć studenci przeprowadzają przykłady
numerycznej analizy wybranych typów sprzężeń z wykorzystaniem
następujących systemów CAE: MSC.Patran/Nastran, MSC.Marc/Mentat, Ansys
Multiphysics
Program przedmiotu
- wykład: 15 godzin w semestrze
- laboratorium: 30 godzin w semestrze
Warunki zaliczenia
- Zaliczenie na
ocenę pozytywną laboratoriów (warunki podaje prowadzący
na zajęciach)
- Egzamin z
wykładu.
OCENA KOŃCOWA: O=0.5E+0.5L
E - ocena z egzaminu (musi być pozytywna)
L - ocena z laboratorium (musi być pozytywna)
Tematyka wykładów
-
Podstawowe definicje i
sformułowania.
-
Podstawowe rodzaje
sprzężeń, przykłady praktyczne
-
Metody numeryczne
(MES, MEB, MRS) w zagadnieniach sprzężonych
-
Sprzężenie pól
termicznych i mechanicznych - termosprężystość
-
Sprzężenie pól
elektrycznych i termicznych
-
Sprzężenie pól
elektrycznych, termicznych i mechanicznych
-
Sprzężenie pól
elektrycznych i mechanicznych - sprzężenie
elektrostatyczno - strukturalne
-
Sprzężenie pól
elektrycznych i mechanicznych - piezolelektryczność
-
Sprzężenie pól
przepływowych i mechanicznych - sprzężenie FSI (ang.
Fluid-Structure interaction)
-
Wybrane zagadnienia
modelowania wieloskalowego w układach termosprężystych
Tematyka laboratoriów
Rozwiązywanie praktycznych zagadnień dotyczących
numerycznego modelowania pól sprzężonych, m.in z
zakresu: termosprężystości, sprzężenia
elektro-termicznego, elektrotermo-mechanicznego,
elektrostatyczno - mechanicznego, piezoelektrycznego.
Literatura
- Beer G., Finite
Element, Boundary Element and Coupled analysis of
Unbounded Problems in Elastostastics, Int. J. Numer.
Meth. Eng., vol. 19, 1983.
- Chandrupatla T.R., Belegundu A.D.,
Introduction to Finite Elements in Engineering,
Prentice-Hall Inc. New Jersey, 1991
- MSC.MARC Theory
and user information Vol. A-E, MSC Software Corporation
2001.
- Ansys Multiphisics
documentation, AnsysCo.
- Zienkiewicz O.C., Taylor R.L. The
Finite Element Method, Vol. 1-2, Butterworth, Oxford
2000.
- Zienkiewicz O. C., Taylor R. L., The
Finite Element Method. Nonlinear, Vol. 2, Butterworth,
Oxford, 2000.
- Zienkiewicz O. C., Taylor R. L., The
Finite Element Method. The Fluid Mechanics, Vol. 3,
Butterworth, Oxford, 2000.
|