Metody heurystyczne
Kierunek:
Mechatronika
Specjalność: Modelowanie i symulacja systemów mechatronicznych
(ME3)
Rodzaj studiów i semestr: stacjonarne II st. sem. III
Punkty ECTS: 2
Prowadzący:
dr hab. inż. Witold Beluch
Opis przedmiotu
Jedną z najważniejszych metod
informatyki jest przeszukiwanie, często utożsamiane ze sztuczną
inteligencję (Artificial intelligence, AI). Często zadania
praktyczne można traktować jako konkretne przypadki ogólnego zadania
przeszukiwania, w szczególności wiele zagadnień technicznych,
ekonomicznych, logistycznych i innych problemów praktycznych ma postać
zadań optymalizacji. Optymalizacja w sensie dokładnym jest poszukiwaniem
najlepszego ze wszystkich możliwych rozwiązań (tzw. optimum globalnego).
Częstokroć rzeczywiste zagadnienia są zbyt skomplikowane, by można je
opisać tradycyjnym modelem matematycznym. Często też wystarczające jest
podanie tzw. rozwiązania quasi-optymalnego, co może być uzasadnione np.
ograniczeniami czasowymi.
W wielu praktycznych problemach, gdy
np. nie jest znana analityczna postać funkcji celu, nie wiadomo
również, jak znalezione rozwiązanie bliskie jest rozwiązaniu
optymalnemu. Istotnym zagadnieniem jest także efektywność algorytmu
poszukiwania najlepszego rozwiązania, mierzona czasem wykonania i
wielkością zajętej pamięci. Dla wielu rodzajów zadań optymalizacji, jak
np. zadanie komiwojażera, nie istnieją efektywne algorytmy
optymalizacji. W związku z
powyższym wiele współczesnych zagadnień optymalizacji rozwiązywanych
jest metodami zaliczanymi do metod heurystycznych czy też metaheurystyk.
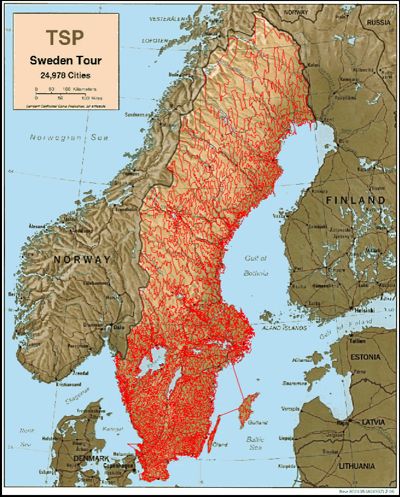
Optymalne rozwiązanie zadania
komiwojażera dla 24978 miast w Szwecji (2004r)
(http://www.tsp.gatech.edu//sweden/index.html)
Heurystyka
(z greckiego: heuresis – odnaleźć, odkryć) to metoda znajdowania
rozwiązań („niepełny algorytm”) która pozwala na znalezienie w
akceptowalnym czasie przynajmniej „dostatecznie dobrego” przybliżonego
rozwiązania problemu. Metod tych używa się np. wtedy, gdy pełny algorytm
jest nieznany lub zbyt kosztowny obliczeniowo.
Z kolei metaheurystyka
to ogólny algorytm (czyli heurystyka) do rozwiązywania problemów
obliczeniowych, zazwyczaj optymalizacyjnych. Określenie oznacza
„heurystykę wyższego poziomu” co wynika z faktu, że algorytmy tego typu
nie rozwiązują bezpośrednio żadnego problemu, a jedynie podają sposób na
utworzenie odpowiedniego algorytmu. Metody te często są inspirowane
mechanizmami biologicznymi czy fizycznymi. Zaliczyć do nich można np.:
algorytmy ewolucyjne, sztuczne sieci neuronowe, systemy rozmyte,
algorytmy immunologiczne czy systemy mrówkowe.
Program przedmiotu
-
Wykład: 15 godzin w semestrze
-
Laboratorium: 15 godzin w semestrze
Warunki zaliczenia
1. Zaliczenie na
ocenę pozytywną ćwiczeń (warunki podaje prowadzący na zajęciach)
2. Kolokwium z
wykładu.
OCENA
KOŃCOWA: O=0.65K+0.35L
K - ocena z
kolokwium (musi być pozytywna)
L - ocena z
laboratorium
Tematyka wykładów
-
Wprowadzenie do metod przeszukiwania. Zagadnienia „łatwe” i „trudne”. Złożoność algorytmu. Przykładowe problemy.
-
Strategie ślepe.
-
Strategie heurystyczne
-
Gry dwuosobowe.
-
Dobór metody heurystycznej.
-
Algorytmy genetyczne (AG) i ewolucyjne (AE).
-
Sztuczne sieci neuronowe (SSN)
-
Zbiory rozmyte, logika rozmyta i systemy rozmyte (SR)
-
Inne metody inteligencji obliczeniowej.
Tematyka
laboratoriów
-
Przeszukiwanie grafów - strategie ślepe.
-
Przeszukiwanie grafów - strategie heurystyczne.
-
Algorytmy ewolucyjne.
-
Sztuczne sieci neuronowe.
-
Sterowanie rozmyte.
-
Problem komiwojażera.
Literatura
-
L.
Rutkowski, Metody i techniki sztucznej inteligencji,
Wydawnictwa Naukowe PWN, Warszawa, 2006.
-
J. Mulawka,
Systemy ekspertowe,
WNT, Warszawa, 1997.
-
J.
Arabas, Wykłady z algorytmów ewolucyjnych, WNT,
Warszawa, 2001.
-
R.
Tadeusiewicz, Elementarne wprowadzenie do techniki
sieci neuronowych z przykładowymi programami, Akad.
Oficyna Wyd. PLJ, Warszawa, 1998.
Odnośniki:
Do pobrania
|