Numeryczne modelowanie pól sprzężonych
Kierunek:
Automatyka i Robotyka, Mechanika i Budowa Maszyn
Semestr: II
Punkty ECTS: 2 (AiR) lub 1 (MiBM)
Specjalność: AB3, MB4, MB2
- Komputerowe wspomaganie projektowania
i eksploatacji maszyn (MB2)
- Mechanika komputerowa (MB4)
- Modelowanie komputerowe układów i
procesów (AB3)
Prowadzący:
dr hab. inż. Adam Długosz
Opis przedmiotuPola
sprzężone to zjawiska o różnej naturze fizycznej, które:
- zachodzą w obszarach, które nie mogą
być od siebie oddzielone,
- żaden zbiór zmiennych opisujących
dane zjawiska fizyczne nie może być wyeliminowany i
zastąpiony poprzez opis układu jednego zjawiska
fizycznego.
Można wyróżnić dwie klasy problemów:
- Sprzężenie następuje na styku
obszarów poprzez warunki brzegowe (Zwykle obszary
opisują różne zjawiska fizyczne, ale możliwe jest
również sprzężenie obszarów w których występuje to samo
lub podobne zjawisko fizyczne przy różnym stopniu ich
dyskretyzacji):
- Obszary, w których zachodzą zjawiska
pokrywają się (częściowo lub zupełnie). Sprzężenie
zachodzi poprzez równania opisujące różne zjawiska
fizyczne.
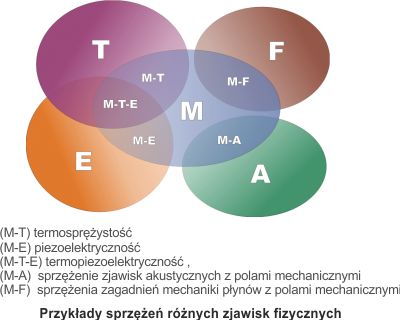
W ramach przedmiotu omawiane są głównie interakcje
pomiędzy polami mechanicznymi i niemechanicznymi.
W ramach zajęć studenci przeprowadzają przykładny
numerycznej analizy wybranych typów sprzężeń z wykorzystaniem
następujących systemów CAE:
- MSC.Patran/Nastran
- MSC.Marc/Mentat
- Ansys Multiphysics
Program
Wykład 30 godzin w semestrze
Warunki zaliczeniaZaliczenie
na ocenę pozytywną testu zaliczeniowego/egzaminacyjnego
Literatura
- Beer G., Finite
Element, Boundary Element and Coupled analysis of
Unbounded Problems in Elastostastics, Int. J. Numer.
Meth. Eng., vol. 19, 1983.
- Chandrupatla T.R., Belegundu A.D.,
Introduction to Finite Elements in Engineering,
Prentice-Hall Inc. New Jersey, 1991
- MSC.MARC Theory
and user information Vol. A-E, MSC Software Corporation
2001.
- Ansys Multiphisics
documentation, AnsysCo.
- Zienkiewicz O.C., Taylor R.L. The
Finite Element Method, Vol. 1-2, Butterworth, Oxford
2000.
- Zienkiewicz O. C., Taylor R. L., The
Finite Element Method. Nonlinear, Vol. 2, Butterworth,
Oxford, 2000.
- Zienkiewicz O. C., Taylor R. L., The
Finite Element Method. The Fluid Mechanics, Vol. 3,
Butterworth, Oxford, 2000.
Linki
|