Statystyka matematyczna i planowanie
eksperymentu
Kierunek:
Mechatronika
Rodzaj studiów i semestr: stacjonarne I st. sem. V
Punkty ECTS: 3
Prowadzący:
prof. dr hab. inż. Ewa
Majchrzak ,
dr hab. inż. Jerzy
Mendakiewicz prof. Pol. Śl.,
dr inż. Marek Jasiński,
dr inż. Grażyna Kałuża,
dr inż. Marek Paruch,
dr inż. Jolanta
Dziatkiewicz, dr inż.
Łukasz Turchan
J. Graunt:
„Wnikliwa analiza liczb prowadzi do ukazania prawidłowości rządzących
zjawiskami, przy założeniu, że jest rozpatrywana w dużej masie”.
Opis przedmiotu
 Statystyka
zajmuje się sposobami gromadzenia danych liczbowych oraz ich analizą Statystyka
zajmuje się sposobami gromadzenia danych liczbowych oraz ich analizą
i interpretacją. Pozwala również na modelowanie zjawisk fizycznych za
pomocą, czarnej skrzynki’’, co wiąże się z poszukiwaniem związków między
zmiennymi wejściowymi
i wyjściowymi. Głównym celem przedmiotu jest przedstawienie metod
estymacji punktowej i przedziałowej oraz wnioskowania statystycznego.
Szczególny nacisk położono na metody analizy regresji i korelacji oraz
zasady planowania eksperymentów. Zdobyte w ramach wykładu informacje
Studenci wykorzystują na zajęciach laboratoryjnych, na których
rozwiązują praktyczne zadania wykorzystując darmowe programy – Calc oraz
Scilab.
Program przedmiotu
-
Wykład: 15 godzin w
semestrze
-
Laboratorium: 15 godzin
w semestrze
Tematyka wykładów
-
Wprowadzenie. Podstawowe pojęcia:
zmienna losowa dyskretna i ciągła,
dystrybuanta zmiennej losowej dyskretnej
i ciągłej, funkcja prawdopodobieństwa,
gęstość prawdopodobieństwa, wartość
oczekiwana, wariancja, odchylenie
standardowe.
-
Rozkłady
zmiennej losowej dyskretnej:
jednopunktowy, dwupunktowy, równomierny,
Bernoulliego, Poissona. Rozkłady
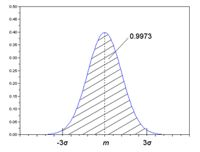
zmiennej losowej ciągłej: równomierny,
normalny, wykładniczy, chi-kwadrat,
gamma, t-Studenta, Weibulla, beta,
F-Snedecora.
-
Estymacja punktowa i przedziałowa.
Własności estymatorów. Estymacja
przedziałowa (3 modele). Weryfikacja
hipotez statystycznych: hipoteza, błąd I
i II rodzaju, test statystyczny.
Hipotezy parametryczne i
nieparametryczne. Przykłady testowania
hipotez statystycznych.
-
Analiza
regresji i korelacji. Regresja liniowa,
wnioskowanie statystyczne na bazie
modelu regresji liniowej, regresja
krzywoliniowa, wnioskowanie statystyczne
na bazie modelu regresji krzywoliniowej.
Liniowy model regresji wielokrotnej.
-
Planowanie eksperymentu. Wprowadzenie.
Plany dwupoziomowe całkowite, połówkowe,
ćwiartkowe – funkcja regresji związana z
każdym planem. Plany trójpoziomowe –
funkcja regresji. Plany D-optymalne,
kompozycyjne. Przykłady planów
eksperymentów.
Tematyka laboratorium
-
Wprowadzenie do Scilaba i Open Office
Calc.
-
Zmienna
losowa – podstawowe pojęcia.
-
Podstawowe rozkłady zmiennych losowych.
-
Teoria
estymacji.
-
Testowanie hipotez statystycznych.
-
Analiza
regresji.
-
Planowanie eksperymentu.
Warunki zaliczenia
-
Szczegółowe warunki podają
prowadzący na zajęciach.
Literatura
-
Andrzej
Stanisz, Przystępny kurs statystyki w oparciu o program
STATISTICA PL na przykładach
z medycyny, tom I, Wydawnictwo StatSoft Polska, Sp. z
o.o., Kraków, 1998; http://www.statsoft.pl.
-
Andrzej
Stanisz, Przystępny kurs statystyki w oparciu o program
STATISTICA PL na przykładach z medycyny, tom II,
Wydawnictwo StatSoft Polska, Sp. z o.o., Kraków, 2000;
http://www.statsoft.pl.
-
Tomasz
Zieliński, Jak pokochać statystykę czyli STATISTICA do
poduszki, Wydawnictwo StatSoft Polska Sp. z o.o.,
Kraków, 1999; http://www.statsoft.pl.
-
Paweł
Kobus, Robert Pietrzykowski, Wojciech Zieliński,
Statystyka z pakietem STATISTICA, Wydawnictwo Fundacja
„Rozwój SGGW”, Warszawa, 1998.
-
Andrzej
Luszniewicz, Teresa Słaby, Statystyka stosowana, Polskie
Wydawnictwo Ekonomiczne, Warszawa, 1997.
-
Zdzisław
Hellwig, Elementy rachunku prawdopodobieństwa i
statystyki matematycznej, Wydawnictwo Naukowe PWN,
Warszawa, 1998.
-
Andrzej
Luszniewicz, Statystyka ogólna, Państwowe Wydawnictwo
Ekonomiczne, Warszawa, 1987.
-
Jerzy
Greń, Statystyka matematyczna, PWN, Warszawa, 1987.
-
Jerzy
Greń, Statystyka matematyczna – modele i zadania, PWN,
Warszawa, 1984.
-
Ryszard
Zieliński, Wojciech Zieliński, Tablice statystyczne,
PWN, Warszawa, 1990.
-
Stanisław
Furdal, Modelowanie statystyczne w badaniach
empirycznych, Wydawnictwo Instytutu Sportu, Warszawa,
1989.
-
Dobiesław
Bobrowski, Probabilistyka w zastosowaniach technicznych,
WNT, Warszawa, 1986.
-
N.R.
Draper, H. Smith, Analiza regresji stosowanej, PWN,
Warszawa, 1973
-
Wojciech
Zieliński, Analiza regresji, Fundacja „Rozwój SGGW”,
Warszawa, 1998.
-
A. Welfe,
Ekonometria, PWN, Warszawa, 1995.
-
C.
Domański, Testy statystyczne, Państwowe Wydawnictwo
Ekonomiczne, Warszawa, 1990.
-
S. Brandt,
Analiza danych, PWN, Warszawa, 1998.
Do pobrania
|