Kierunek: Automatyka i robotyka
Semestr: III i IV
Punkty ECTS: 4 (sem.III) i 5 (sem.IV)
Prowadzący: dr hab. inż. Witold Beluch

Opis przedmiotu

Odkształcalność typowych materiałów konstrukcyjnych jest zazwyczaj mała, jednakże niepomijalna, np:

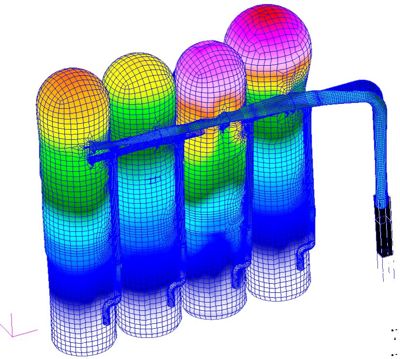
Nagrzewnice wielkiego pieca, układ odkształcony (przeskalowany), wys. ok. 15m.

Wytrzymałość materiałów jest działem mechaniki, który zajmuje się ciałami odkształcalnymi. Obejmuje teoretyczne jak i doświadczalne badania procesów odkształcania i niszczenia ciał poddanych różnorodnym obciążeniom. Prowadzi to do analizy zachowania się konstrukcji pod działaniem obciążeń (tzw. praca konstrukcji).

Analiza taka pozwala zaprojektować konstrukcję tak, by mogła poprawnie pracować tworząc jednocześnie układ racjonalnie zaprojektowany. Projektowanie polega na doborze: a) kształtu; b) materiału; c) wymiarów konstrukcji. 

Do sił działających na konstrukcję zalicza się: a) siły zewnętrzne; b) ciężar (siły masowe); c) siły przekazywane przez współpracujące elementy; d) tarcie; e) zmiany temperatury; f) opory powietrza; g) parcie cieczy; h) skurcz; i) pęcznienie; j) korozję.

Przy ocenie konstrukcji należy sprawdzić następujące warunki:

• Warunek wytrzymałości - w całym elemencie obciążenia nie mogą spowodować osiągnięcia wytrzymałości materiału.

• Warunek sztywności - dotyczy występowania dużych odkształceń, uniemożliwiających normalną eksploatację konstrukcji (nawet mimo spełnienia pkt. 1).

• Warunek stateczności - spełnienie go ma zapobiec nagłym zmianom kształtu lub położenia pręta (nawet mimo spełnienia pkt. 1).

Metody, z jakich korzysta wytrzymałość materiałów, można podzielić na 3 główne grupy:

• Metody doświadczalne – laboratoryjne badania wytrzymałościowe pozwalają określić własności materiału i wyznaczyć parametry charakteryzujące jego odkształcalność.

• Metody analityczne – umożliwiają wyznaczenie takich wielkości, jak przemieszczenia, odkształcenia czy naprężenia na drodze obliczeń analitycznych;

• Metody numeryczne – dla większości rzeczywistych konstrukcji uzyskanie wyników na drodze obliczeń analitycznych jest niemożliwe bądź prowadzi do zbyt daleko idących uproszczeń. Powszechnie stosuje się numeryczne metody przybliżone, jak metoda elementów skończonych (MES) czy metoda elementów brzegowych (MEB). Metody te pozwalają uwzględnić w zasadzie dowolny stopień skomplikowania konstrukcji.

Obliczeniom (analitycznym bądź numerycznym) podlegają modele układów rzeczywistych. W układach mechanicznych niezbędne są następujące modele:

•  model materiału – np. ośrodek ciągły sprężysto-plastyczny;

•  model postaci (kształtu) – np. pręt, powłoka, tarcza, płyta;

•  model obciążenia – np. siła skupiona, siła powierzchniowa;

•  model złomu (pęknięcia, zniszczenia) – np. złom spowodowany obciążeniem statycznym, kruche pękanie.

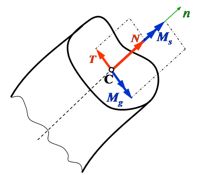Najczęściej stosowanym modelem postaci jest pręt.

Wyróżnia się 4 proste przypadki wytrzymałościowe:

• Rozciąganie – jedyną siła wewnętrzną w przekroju poprzecznym pręta jest siła normalna N.

• Ścinanie – jedyną siła wewnętrzną w przekroju poprzecznym pręta jest siła poprzeczna (tnąca) T.

• Skręcanie – jedyną siła wewnętrzną w przekroju poprzecznym pręta jest moment skręcający Ms.

• Zginanie – jedyną siła wewnętrzną w przekroju poprzecznym pręta jest moment gnący Mg.

Szczególne znaczenie w wytrzymałości materiałów ma od wielu lat metoda elementów skończonych, czyli w skrócie MES. Jest to metoda numeryczna, która wraz z rozpowszechnieniem się komputerów osobistych spowodowała prawdziwą rewolucję w zakresie obliczeń wytrzymałościowych. O ile dawniej w inżynierskich obliczeniach wytrzymałościowych dominowały z konieczności modele najprostsze, czyli pręty i układy prętowe, to obecnie dzięki MES powstały liczne systemy programów komputerowych umożliwiające przybliżoną analizę wytrzymałościową nawet najbardziej skomplikowanych modeli ciał odkształcalnych (elementów maszyn i budowli).

---

Semestr zimowy:
- wykład: 30 godzin w semestrze
- ćwiczenia: 15 godzin w semestrze

Semestr letni:
- ćwiczenia: 15 godzin w semestrze
- laboratorium: 30 godzin w semestrze

Tematyka wykładów

Tematyka ćwiczeń

1. Rozciąganie prętów prostych
   Obliczanie sił wewnętrznych, naprężeń i wydłużeń części i całego pręta,
   analiza prętów statycznie niewyznaczalnych – warunki równowagi, związki fizyczne i związki geometryczne, obliczenia wytrzymałościowe prętów – sprawdzenie warunku wytrzymałości i sztywności, dobór materiału, określenie obciążenia dopuszczalnego i wymiarów pręta.
   
2. Skręcanie prętów o przekroju kołowym:
   Obliczanie momentów skręcających, naprężeń stycznych i kątów skręcenia w obracającym się wale, obliczanie momentów utwierdzenia, momentów skręcających, kątów obrotu przekrojów w pręcie statycznie niewyznaczalnym.
   
3. Parametry geometryczne przekrojów prętów prostych:
   Obliczanie momentów statycznych przekroju, współrzędnych środka ciężkości,
   momentów bezwładności i zboczenia przekroju, określenie kierunków głównych osi bezwładności i głównych centralnych momentów bezwładności.
   
4. Siły wewnętrzne w belkach:
   Wyznaczanie momentów gnących i sił poprzecznych w belkach, wykresy sił wewnętrznych, zależności różniczkowe między siłami wewnętrznymi.
   
5. Zginanie belek – obliczenia wytrzymałościowe:
   Obliczanie wskaźnika wytrzymałości przekroju na zginanie, maksymalnych naprężeń normalnych w przekroju, dobór wymiarów przekroju lub dopuszczalnego obciążenia.
   
6. Zginanie belek – równanie różniczkowe osi ugiętej:
   Wyznaczanie przemieszczeń belek statycznie wyznaczalnych przy wykorzystaniu równania różniczkowego osi ugiętej i metody Clebscha, wyznaczenie reakcji nadliczbowych i wyznaczanie przemieszczeń dla belek statycznie niewyznaczalnych przy wykorzystaniu metody Clebscha.
   
7. Wytrzymałość złożona:
   Obliczanie naprężeń zredukowanych w prętach jednocześnie zginanych i skręcanych oraz w prętach jednocześnie rozciąganych (ściskanych) i zginanych. Wyznaczanie wymiarów przekroju z warunku wytrzymałościowego.
   
8. Metody energetyczne:
   Obliczanie przemieszczeń w w statycznie wyznaczalnych płaskich układach  prętowych przy wykorzystaniu twierdzenia Castigliana i metodą Maxwella-Mohra. Obliczanie nadliczbowych reakcji podporowych w statycznie niewyznaczalnych płaskich układach  prętowych  przy wykorzystaniu twierdzenia Menabrei-Castigliana.
   
9. Wyboczenie pręta prostego:
   Obliczanie układów narażonych na zjawisko utraty stateczności w zakresie sprężystym (wykorzystanie wzoru Eulera) i w zakresie sprężysto-plastycznym (wykorzystanie wzorów Tetmajera-Jasińskiego i Johnsona- Ostenfelda).

Zajęcia laboratoryjne

Literatura

• R. Bąk, T. Burczyński: Wytrzymałość materiałów z elementami ujęcia komputerowego, WNT, Warszawa, 2001.
• Z. Dyląg, A.Jakubowicz, Z.Orłoś: Wytrzymałość materiałów. Tom 1 i 2, WNT, Warszawa, 1996.
• R. Bąk: Piętnaście wykładów z wytrzymałości materiałów. Wydawnictwo Politechniki Śląskiej, Gliwice, 1996.
• W. Szuścik, J. Kuczyński: Metodyczny zbiór zadań z wytrzymałości materiałów, cz.2, wyd. 2, Skr. Uczel. Pol. Śl., Nr 1918, Gliwice, 1995.
• M.E. Niezgodziński, T. Niezgodziński: Zadania z wytrzymałości materiałów, WNT, Warszawa, 1997.
• M. Banasiak, K. Grossman, M. Trombski: Zbiór zadań z wytrzymałości materiałów, PWN, Warszawa, 1998.

Odnośniki:

• http://www.mes.polsl.pl/ - Programy komputerowe MES do książki: R.Bąk, T.Burczyński „Wytrzymałość materiałów z elementami ujęcia komputerowego”.

• http://limba.wil.pk.edu.pl/~az/uzupeln.php - uzupełnienia do wykładu z wytrzymałości materiałów, Politechnika Krakowska.