Kierunek: Mechatronika
Semestr: II
Punkty ECTS: 2
Prowadzący: dr inż. Jacek Ptaszny

Cel przedmiotu

Celem wykładu jest dokonanie przeglądu klasycznych oraz nowoczesnych metod optymalizacji. Celem laboratorium jest badanie efektywności różnych metod optymalizacji oraz zastosowanie wybranych metod do rozwiązywania praktycznych zagadnień inżynierskich.

Program przedmiotu

• Wykład: 15 godzin w semestrze
• Laboratorium: 15 godzin w semestrze

Tematyka wykładów

• Wiadomości podstawowe (historia, definicja i zastosowanie metod optymalizacji, sformułowanie zagadnienia optymalizacji, klasyfikacja modeli matematycznych układów i procesów, dobór zmiennych projektowych, funkcja celu i jej własności, zbiór rozwiązań dopuszczalnych, klasyfikacja zagadnień i metod optymalizacji).
• Deterministyczne metody bezgradientowe optymalizacji funkcji jednej zmiennej (metody: złotego podziału, Fibonacciego, interpolacji kwadratowej) oraz funkcji wielu zmiennych (metody: Hooke’a-Jeevesa, Rosenbrocka, simpleks Neldera-Meada, Gaussa-Seidela, Powella).
• Definicja i metody analizy wrażliwości (metody: bezpośrednia, układu sprzężonego).
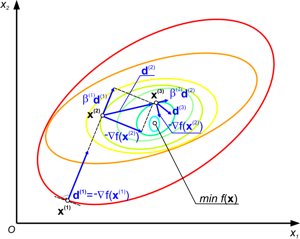
• Metody gradientowe pierwszego rzędu (metody: największego spadku, gradientów sprzężonych) i drugiego rzędu (metody: Newtona, zmiennej metryki).
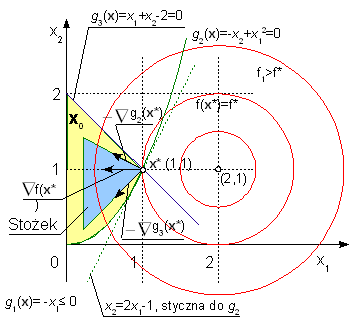
• Metody optymalizacji z ograniczeniami (metody: Lagrange’a, Karusha-Kuhna-Tuckera, funkcji kary).
• Optymalizacja wielokryterialna (podejście Pareto, redukcja zagadnień wielokryterialnych).
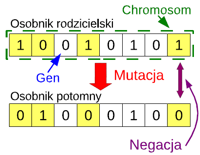
• Niedeterministyczne metody optymalizacji (metoda Monte Carlo, symulowane wyżarzanie, algorytmy genetyczne i ewolucyjne, strategie ewolucyjne, sztuczne systemy immunologiczne, algorytmy rojowe, poszukiwanie harmonii).
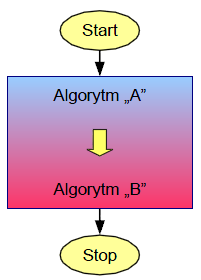
• Hybrydowe metody optymalizacji.
• Przykłady optymalizacji i identyfikacji układów mechanicznych i procesów technologicznych.

Tematyka laboratorium

• Testowanie metod gradientowych zaimplementowanych w programie komputerowym "Genetyka"
• Optymalizacja gradientowa za pomocą programu "Scilab"
• Optymalizacja globalna za pomocą algorytmu ewolucyjnego
• Optymalizacja globalna za pomocą sztucznych systemów immunologicznych
• Optymalizacja globalna za pomocą systemów rojowych
• Porównanie efektywności wybranych metod w optymalizacji lub identyfikacji  układów mechanicznych
• Kolokwium

Warunki zaliczenia

• Po każdych dwóch wykładach następuje sprawdzian wiadomości w postaci kartkówki. Oceną końcową z wykładu jest średnia arytmetyczna ocen z kartkówek.
• Na ostatnim laboratorium odbywa się kolokwium, na którym student uzyskuje ocenę z tej formy przedmiotu.
• Oceną końcową z przedmiotu jest średnia arytmetyczna ocen z wykładu oraz laboratorium.
   

Literatura

1. Arabas J., Wykłady z algorytmów ewolucyjnych. WNT, Warszawa, 2004.

2. Findeisen W., Szymanowski J., Wierzbicki A., Teoria i metody obliczeniowe optymalizacji. PWN 1980.

3. Geem Z.W., Music-inspired harmony search algorithm. Theory and applications. Springer Verlag, Berlin Heidelberg, 2009.

4. Gürdal Z., Haftka R. T., Elements of structural optimization. Kluwer Academic Publishers, Dordrecht – Boston – London, 1992.

5. Kusiak J., Danielewska-Tułecka A., Oprocha P., Optymalizacja. Wybrane metody z przykładami zastosowań. PWN, Warszawa, 2009.

6. Michalewicz Z., Algorytmy genetyczne + struktury danych = programy ewolucyjne. WNT, Warszawa, 1999.

7. Wierzchoń S.T., Sztuczne systemy immunologiczne. Teoria i zastosowania. Wydawnictwo EXIT, Warszawa, 2001.

8. Orantek P. , Zastosowanie algorytmów hybrydowych w zagadnieniach optymalizacji i identyfikacji dynamicznych układów mechanicznych. Rozprawa doktorska, Politechnika Śląska, KWMiMKM, Gliwice, 2002.

Do pobrania